1. If the compound interest on a certain sum for 2 years in Rs. 80.80 and the simple interest Rs. 80; then the rate of interest per annum is
1. 2%
2. 1%
3. 3%
4. 4%
[expand title=”Answer & Explanation”]
Answer:- 1
Explanation :-
Let the sum be P and Rate of Interest be R% per annum
SI on Rs.P for 2 years = 80
(PRT)/100 = 80
(PR×2/100) = 80
(PR/50) = 80
PR = 4000
Difference between CI & SI = Rs. 80.80 – Rs. 80 = Rs. 0.80
Difference between CI & SI = P(R/100)^2 = 0.80
(PR^2)/10000 = 0.80
(PR^2)= 8000
PR×R = 8000
4000×R = 8000 (by putting value of PR=4000)
R = 8000/4000 = 2%
[/expand]
2. The compound interest on a sum for 2 years is Rs. 832 and the simple interest on the same sum for the same period is Rs. 800. The difference between the compound and simple interest for 3 years will be
1. Rs. 48
2. Rs. 66.56
3. None of these
4. Rs. 98.56
[expand title=”Answer & Explanation”]
Answer:- 4
Explanation :-
Difference Between C.I and S.I in 2years = Rs. (832 – 800) = Rs.32
S.I for 1 year =Rs.800/2 = Rs. 400
S.I for Rs.400 for one year =Rs.32
rate = [(100*32)/(400*1)% = 8%
Difference between C.I and S.I for 3rd year = S.I on Rs.832
=> Rs.(832*8*1)/100 = Rs.66.56
Total difference between the CI & SI for 3 years
=> 32 + 66.56 = Rs.98.56
[/expand]
3. On a certain sum of money, the simple interest for 2 years is Rs. 200 at the rate of 7% per annum. Find the difference in C.I. and S.I.
1. None of these
2. Rs. 9
3. Rs. 7
4. Rs. 11
[expand title=”Answer & Explanation”]
Answer:- 3
Explanation :-
P = ? R = 7% T = 2 Years SI = 200
P =(100×SI)/RT = (100×200)/(7×2) = Rs.10000/7
CI = [ P(1+R/100)^T]−P = [ P(1+7/100)^2] − P
=> P[(1+7100)2−1] = P(1+(14/100)+(49/10000)−1) = P [ (14/100)+(49/10000) ]
=> (10000/7) [ (14/100)+(49/10000) ] = 200+7 = Rs. 207
Difference (CI – SI) = 207 – 200 = Rs.7
OR
The difference between CI and SI on Rs. P for 2 years at R% p.a. = (R×SI) / (2×100)
Therefore , CI – SI =(7×200) / (2×100) = Rs. 7
[/expand]
4. John invested money in two schemes A and B offering compound interest @ 5 p.c.p.a. and 10 p.c.p.a. respectively. If the total amount of interest accrued through two schemes together in two years was Rs. 2075 and the total amount invested was Rs. 15,000, find out the amount invested in Scheme A?
1. Rs. 10000
2. Rs. 8000
3. Rs. 12000
4. Rs. 14000
[expand title=”Answer & Explanation”]
Answer:- 1
Explanation :-

[/expand]
5. A sum of money on compound interest amounts to Rs. 8240 in 2 years and Rs. 9888 in 3 years. The rate of interest is
1. 10%
2. 25%
3. 20%
4. 12%
[expand title=”Answer & Explanation”]
Answer:- 3
Explanation :-
Amount After 2 years = Rs.8240
Therefore , P(1+R/100)^2 = 8240 —————(1)
Amount After 3 years = Rs.9888
P(1+R/100)^3 = Rs.9888 —————(2)
Dividing (2) by (1)
P(1+R/100)^(3-2) = 9888/8240
(1+R/100) = 9888/8240
R = 20%
OR
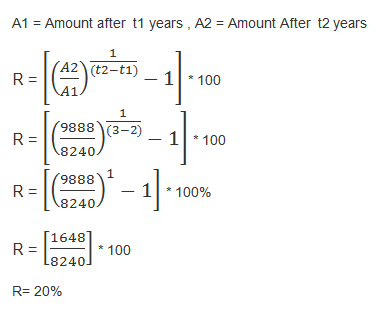
[/expand]
