1. A sum is invested at compounded interest payable annually. The interest in the first two successive years was Rs. 400 and Rs. 420. The sum is
1. Rs. 8000
2. Rs.7500
3. Rs. 8500
4. Rs. 8200
Answer & Explanation Answer:- 1 Explanation :- SI (for 1 year) = 420 -400 = Rs. 20 2. Arun borrowed a certain sum from Manish at a certain rate of simple interest for 2 years. He lent this sum to Sunil at the same rate of interest compounded annually for the same period. At the end of two years, he received Rs. 2400 as compound interest but paid Rs. 2000 only as simple interest. Find the rate of interest. Answer & Explanation Answer:- 1 Explanation :- 3. If a sum on compound interest becomes three times in 4 years, then with the same interest rate, the sum will become 81 times in: Answer:- 3 Explanation :- The sum P becomes 3P in 4 years on compound interest 4. Divide Rs. 3364 between A and B, so that A’s Share at the end of 5 years may equal to B’s share at the end of 7 years, compound interest being at 5 percent. Answer & Explanation Answer:- 1 Explanation :- Let A’s present Share = x & B’s present Share = y 5. A sum is invested for 3 years compounded at 5%, 10% and 20 % respectively. In three years, if the sum amounts to Rs. 1386, then find the sum. Answer & Explanation Answer:- 4 Explanation :- 1386 = P (1+5/100) (1+10/100) (1+20/100)
Rate = (20*100) / (400 * 1) = 5%
SI on the sum for 1st year = Rs.400
Sum = (400*100)/(5*1) = Rs. 8000
1. 40%
2. 30%
3. 20%
4. 10%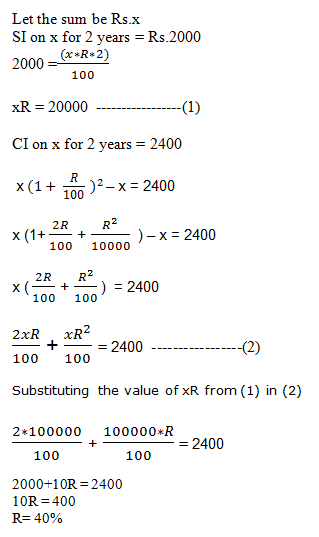
1. 12 years
2. 18 years
3. 16 years
4. 14 years
3P = P(1+R/100)4
⇒ 3 = (1+R/100)4
Let the sum P becomes 81P in n years
81P = P(1+R/100)n
=> 81 = (1+R/100)n
=> (3)4 = (1+R/100)n
=> ((1+R/100)4)4 = (1+R/100)n
=> (1+R/100)16 = (1+R/100)n
Therefore n=16
i.e, the sum will become 81 times in 16 years
1. Rs. 1764 and Rs.1600
2. Rs. 1756 and Rs.1608
3. Rs. 1722 and Rs.1642
4. None of these
A’s share (end of 5 years) = B’s share ( end of 7 years)
x * (1+ 5/100)^5 = y * (1+ 5/100)^7
x/ y = [1+(5/100)]^(7−5)
x/y = [1+(5/100)]^2
x/y = (21/22)^2
x/y = 441/400
x+y = 441+400 = 841
Total Amount = 3364 , Therefore
x = (3364/841)*441= Rs.1764
A’s present Share = Rs.1764
y = (3364/841)*400 = Rs.1600
B’s present Share = Rs.1600
1. Rs. 1500
2. Rs. 1400
3. Rs. 1200
4. Rs. 1000
1386 = P (21/20) (11/10) (6/5)
P = (1386 × 20 × 10 × 5)/(21 × 11 × 6)
P = (66 × 20 × 10 × 5)/(11×6) = 20×10×5 = Rs. 1000
