1. A lends Rs. 1500 to B and a certain sum to C at the same time at 8% per annum simple interest. If after 4 years, A altogether receives Rs. 1400 as interest from B and C, then the sum lent to C is
1. Rs.2875
2. Rs.1885
3. Rs.2245
4. Rs.2615
Answer & Explanation Answer:- 1 Explanation :- Lets suppose Money lent to C be Rs. x 2. A sum of Rs. 10 is given as a loan to be returned in 6 monthly installments at Rs.3. What is the rate of interest? Answer & Explanation Answer:- 4 Explanation :- 3. If the simple interest on a certain sum of money after 3 1⁄8 years is 1⁄4 of the principal, what is the rate of interest per annum? Answer & Explanation Answer:- 3 Explanation :- Let the sum of money be Rs. x 4. If a sum of Rs. 9 is lent to be paid back in 10 equal monthly installments of re. 1 each, then the rate of interest is Answer & Explanation Answer:- 4 Explanation :- 5. Divide Rs. 2379 into 3 parts so that their amount after 2,3 and 4 years respectively may be equal, the rate of interest being 5% per annum at simple interest. The first part is Answer & Explanation Answer:- 1 Explanation :- Let the parts be x, y and z OR Let the parts be x (for2 years), y (for 3 years) and z(for 4 years)
SI (for B) = (1500*8*4)/100 = 480
SI (for C) = (x*8*4)/100 = (32x)/100
Total Interest = 1400
Therefore, 480+(32x/100) = 1400
32x/100 = 920
x = Rs. 2875
1. 820%
2. 620%
3. 780%
4. 640%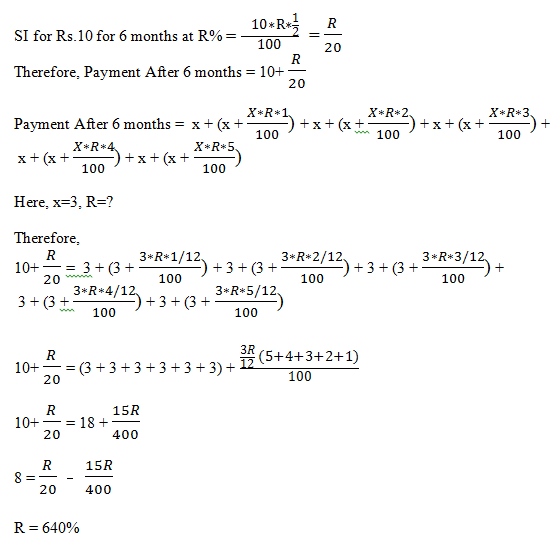
1. 6%
2. 4%
3. 8%
4. 12%
Time = 3 1⁄8 Years = 25⁄8 Years
SI = x⁄4
Therefore, SI = ((P*R*T)/100))
x/4 = (x*R*25/8)/100
R = (x*100*8)/(x*R*25)
R = 8%
1. 11.33%
2. 11%
3. 266.67%
4. 26.67%
1. Rs. 828
2. Rs. 746
3. Rs. 248
4. Rs. 1024
R = 5%
x + SI on x (for 2 years) = y + SI on y (for 3 years) = z + SI on z (for 4 years)
(x+(x*5*2)/100) = (y+(y*5*3)/100) = (z+(z*5*4)/100))
(x+x/10) = (y+3y/20) = (z+z/5)
(11x/10) = (23y/20) = (6z)/5
Let (11x/10) = (23y/20)=(6z/5) = k (where k is a constant)
Therefore, x=(10k/11) , y=(20k/23) , z=(5k/6)
we know that x + y + z = 2379
(10k/11) + (20k/23) + (5k/6)=2379
(10k×23×6) + (20k×11×6) + (5k×11×23) = (2379×11×23×6)
1380k + 1320k + 1265k = 2379×11×23×6
3965k = 2379×11×23×6
k=(2379×11×23×6)/3965
first part, x = 10k/11 = (10/11)×(2379×11×23×6)/3965
x=828
R = 5%
Therefore
R on x = 10%. R on y = 15%. R on z = 20%.
110% of x =115% of y = 120% of z
x/y = 115/110 = 23/22 , x/z = 120/110 = 24/22
=>x : y : z = (23*24):(22*24):(22*23)
x : y : z = 276:264:253 & here x + y + z = (276+264+253) = 793
but x + y + z = 2379 (given)
Therefore
x = (2379/793)*276 = Rs.828
