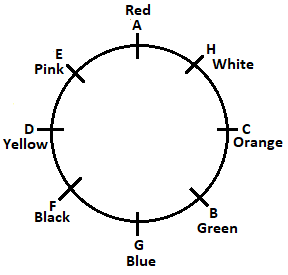
I. Study the following information carefully to answer the given questions.
There are eight friends A, B, C, D, E, F, G, and H sitting around a circular table facing the centre but not necessarily in the same order. All of them have a favourite Colour. Their favourite colours are Red, Green, Yellow, Blue, Black, Orange, Pink and White.
A likes Red and is not an immediate neighbour of the one who likes the orange colour.
The one who likes the Blue colour sits on the immediate left of B, who likes the Green.
C likes the orange colour and sits third to the left of E. The one who likes the White and one who likes the Red are immediate neighbours of each other.
The one who likes the Black and the one who likes the Blue are immediate neighbours of each other but both of them are the neighbours neither of E nor of C.
Neither E nor D likes the White. Only F sits between the one who likes the Blue colour and the one who likes the yellow colour. G sits third to the left of the person who likes the White colour.
Explanation
1. Who likes the Black colour?
A. F
B. G
C. H
D. Can’t be determined
E. None of these
2. E likes which of the following colour?
A. Red
B. Pink
C. Yellow
D. Can’t be determined
E. None of these
3. Which of the following sits exactly between B and H?
A. The person who likes Green
B. The person who likes White
C. The person who likes Orange
D. Black
E. None of these
4. How many persons sit between D and the person who likes the Orange?
A. None
B. One
C. Two
D. Three
E. None of these
5. Which of the following pairs are the immediate neighbour of that person who likes white?
A. B, C
B. A, B
C. E, A
D. D, G
E. C, A
1. A. F
2. B. Pink3.
3. C. The person who likes Orange
4. D. Three
5. E. C, A